bercodes.blogg.se - Special right triangles

Doubling this gives 18 3 for the hypotenuse.Īnother warning flag with 30-60-90 triangles is that you can become so engrossed in the three properties that you lose sight of the triangle itself. Unless your directions are to provide a decimal answer, this can be your final answer for the length of the short side.

Multiply both numerator and denominator times 3: The rules of mathematics do not permit a radical in the denominator, so you must rationalize the fraction.

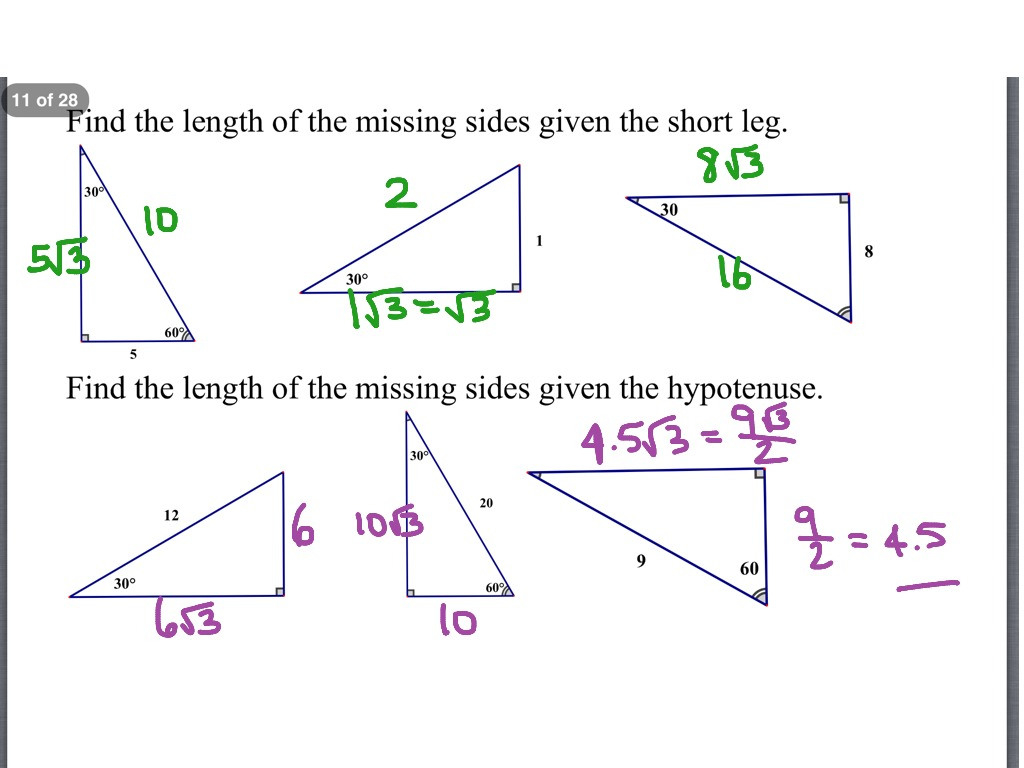
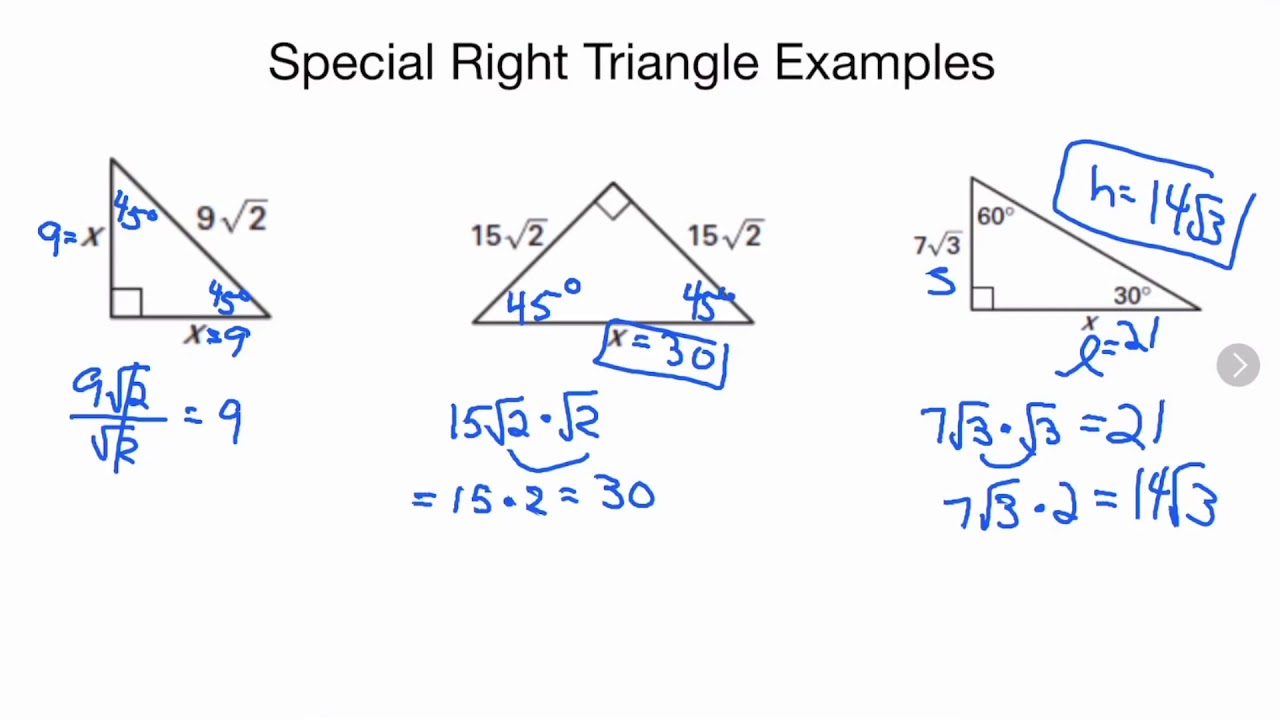
You leap into the problem since getting the short leg is simply a matter of dividing the long leg by the square root of 3, then doubling that to get the hypotenuse.īut you cannot leave the problem like this: What if the long leg is labeled with a simple, whole number? You will notice our examples so far only provided information that would "plugin" easily using our three properties. Work carefully, concentrating on the relationship between the hypotenuse and short leg, then short leg and long leg. That relationship is challenging because of the square root of 3. When working with 30-60-90 triangles, you may be tempted to force a relationship between the hypotenuse and the long leg. This table of 30-60-90 triangle rules to help you find missing side lengths: 30-60-90 Triangle Rules If you know. You can create your own 30-60-90 Triangle formula using the known information in your problem and the following rules. The length of the hypotenuse is always twice the short leg's length. The long leg is the short leg times 3, so can you calculate the short leg's length? Did you say 5? We set up our special 30-60-90 to showcase the simplicity of finding the length of the three sides. We also know that the long leg is the short leg multiplied times the s q u a r e r o o t o f 3: We know that the hypotenuse of this triangle is twice the length of the short leg: Wisdom is knowing what to do with that knowledge.

Two 30-60-90 triangles sharing a long leg form an equilateral triangleĮducation is knowing that 30-60-90 triangles have three properties laid out in the theorem.

Other interesting properties of 30-60-90 triangles are:

If you know the length of any one side of a 30-60-90 triangle, you can find the missing side lengths.

The length of the longer leg is the short leg's length times 3.

The hypotenuse (the triangle's longest side) is always twice the length of the short leg.

These three special properties can be considered the 30-60-90 triangle theorem and are unique to these special right triangles:

Long side (opposite the 60 degree angle) = x 3.

Hypotenuse (opposite the 90 degree angle) = 2 x.

Short side (opposite the 30 degree angle) = x.

The ratio of the sides follow the 30-60-90 triangle ratio: Table Of ContentsĪ 30-60-90 degree triangle is a special right triangle, so it's side lengths are always consistent with each other.

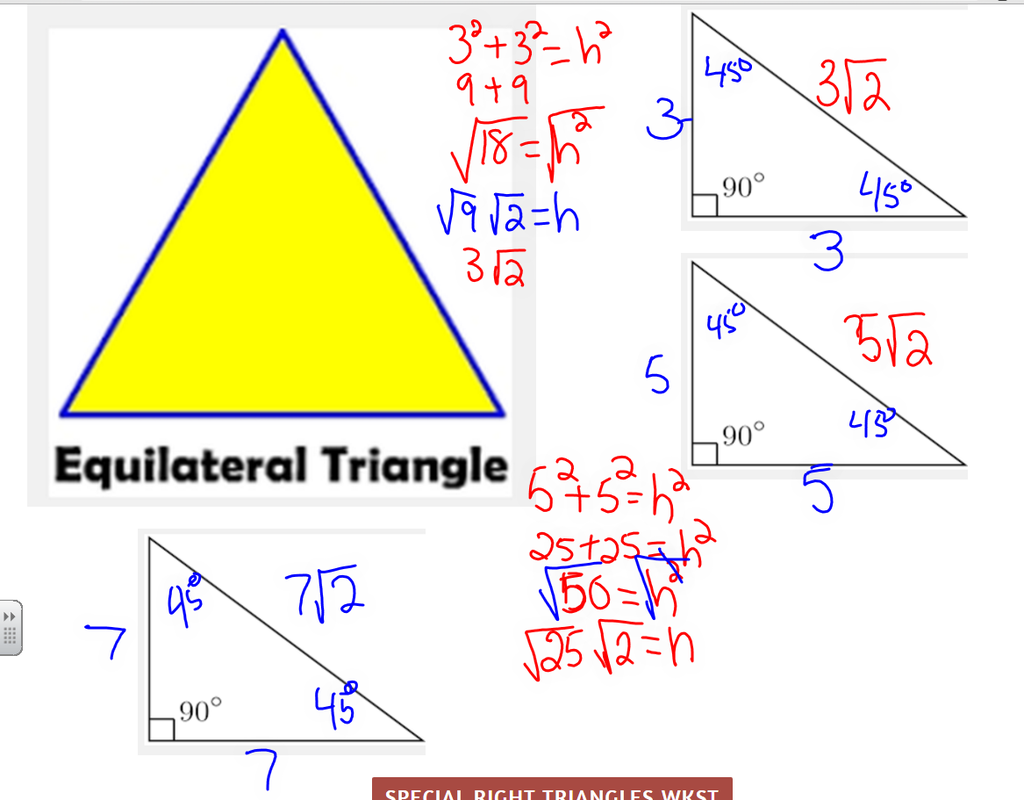
In a right triangle, recall that the side opposite the right angle (the largest angle) is called the hypotenuse (the longest side, and the other two sides are called legs. This means, of the three interior angles, the largest interior angle is opposite the longest of the three sides, and the smallest angle will be opposite the shortest side. The greater the angle, the longer the opposite side. In all triangles, the relationships between angles and their opposite sides are easy to understand. Special triangles in geometry because of the powerful relationships that unfold when studying their angles and sides. Right triangles with 30-60-90 interior angles are known as special right triangles. A 30-60-90 triangle is a right triangle where the three interior angles measure 30 °, 60 °, and 90 °.